pura matematica: Trigonometría

Trigonometría

La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos".
En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Funciones trigonometricas:
La trigonometría como rama de las matemáticas realiza su estudio en la relación entre los lados y ángulos de un triángulo rectángulo, con una aplicación inmediata en geometría y sus aplicaciones. Para el desarrollo de este fin se definieron una serie de funciones que han sobrepasado su fin original, convirtiéndose en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.

Razones trigonometricas:

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo $\alpha \,$ , correspondiente al vértice A, situado en el centro de la circunferencia.

El seno (abreviado como sen, o sin por llamarse "senos" en latín) es la razón entre el cateto opuesto sobre la hipotenusa,

$\operatorname {sen} \, \alpha = \frac{\overline{CB}}{\overline{AB}} = \frac{a}{c}$

El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa,

$\cos\alpha = \frac{\overline{AC}}{\overline{AB}} = \frac{b}{c}$

La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente,

$\tan\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{a}{b}$

Identidad fundamental de la trigonometria:
las identidades trigonométricas verificables para cualquier valor permisible de la variable o variables que se consideren (es decir, para cualquier valor que pudieran tomar los ángulos sobre los que se aplican las funciones).De las definiciones de las funciones trigonométricas:

$\tan{x} = \frac {\operatorname{sen}{x}} {\cos{x}} \qquad \cot{x} = \frac{1} {\tan{x}} = \frac{\cos{x}}{\operatorname{sen}{x}}$

$\sec{x} = \frac{1} {\cos{x}} \qquad \csc{x}= \frac{1}{\operatorname{sen}{x}}$

Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros por cos², se tiene:

$\tan^2\left(x\right)+1 = \sec^2\left(x\right)$

Calculando la recíproca de la expresión anterior:

$\cot^2\left(x\right) + 1 = \csc^2\left(x\right)$

pura matematica

sábado, 2 de abril de 2011

Trigonometría

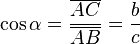
No hay comentarios:

Publicar un comentario